Have you ever tried to walk through a city, crossing every bridge exactly once without retracing your steps? That was the essence of a centuries-old puzzle that not only baffled the residents of Königsberg but also sparked the birth of a whole new branch of mathematics—graph theory.

In this blog, we’ll explore the fascinating story behind the Seven Bridges of Königsberg, the mathematical genius who cracked it, and the powerful ideas it gave rise to.

The Setting: A City of Bridges

Map of Königsberg in 1736

The city of Königsberg (modern-day Kaliningrad, Russia) was built around the Pregel River, which split the city into four distinct land masses connected by seven bridges:

1. Two islands in the river.

2. Two riverbanks on either side.

The challenge that intrigued many locals:
Is it possible to take a walk through the city, crossing each of the seven bridges exactly once and returning to your starting point?

This wasn’t just a riddle—it became a famous problem that stumped many people for years.

Leonhard Euler: The Father of Graph Theory

In 1736, the renowned Swiss mathematician Leonhard Euler was approached with the problem. Instead of solving it through trial and error, he did something revolutionary: he abstracted the city into a mathematical model.

• He represented each land mass as a node (vertex).

• He represented each bridge as a connection (edge) between the nodes.

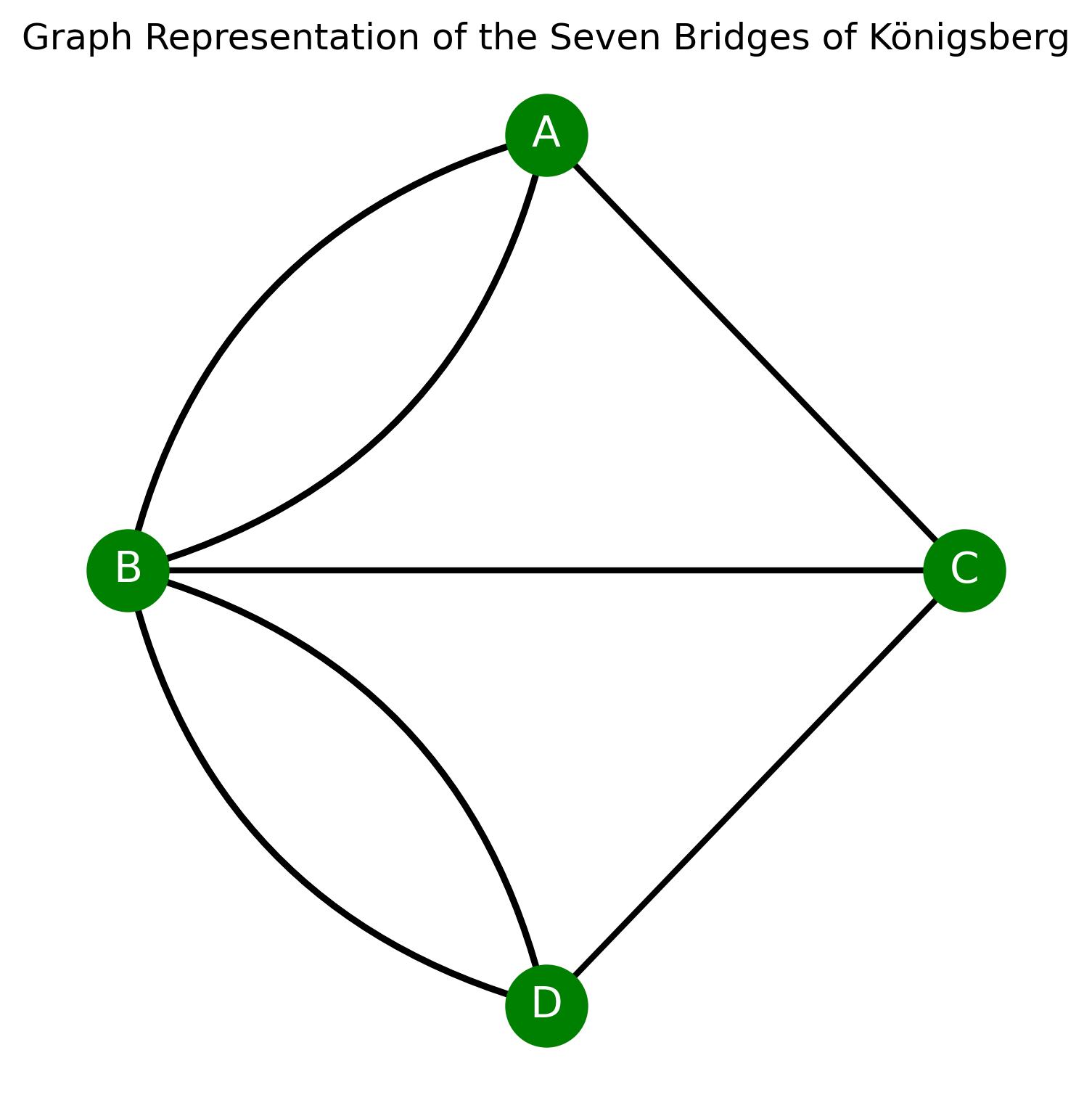
Euler simplified the entire geography into a network of dots and lines, which we now call a graph.

Euler’s Insight

Euler realized that the solution didn’t depend on the exact layout of the city or the length of the bridges—it was all about how the bridges connected the land masses.

Here’s what he found:

• In order to cross each bridge exactly once, every land mass (node) must have an even number of bridges (edges) connected to it—except for two nodes if you’re allowed to start and end at different points.

• This condition ensures that you can enter and exit each node without getting stuck.

In Königsberg:

• All four land masses had an odd number of bridges.

Therefore, Euler concluded:

It is impossible to walk through the city and cross every bridge exactly once.

This was a profound moment. Euler had not just solved the puzzle—he had created a new mathematical language for studying networks.

The Birth of Graph Theory

Euler’s paper on the Königsberg bridges laid the groundwork for what is now called graph theory—a field used to analyze everything from social networks and computer circuits to logistics, airline routes, and even disease spread.

Today, graph theory is a core part of discrete mathematics and computer science, and it all started with a seemingly simple question about walking across some bridges.

Lessons from the Problem

1. Abstraction is powerful: Euler didn’t need maps or measurements—he saw the structure behind the problem.

2. Mathematics reveals impossibility: Sometimes, proving something cannot be done is just as important as finding a way to do it.

3. Simple questions can lead to big ideas: The curiosity of ordinary people about their city led to a major mathematical breakthrough.

Conclusion

Euler’s work on the Seven Bridges is often considered the first true theorem of graph theory. His 1736 paper, titled Solutio problematis ad geometriam situs pertinentis (Solution to a problem relating to the geometry of position), is seen as the beginning of topology and network theory as well.

The Königsberg Seven Bridges Problem is more than a puzzle—it's a landmark in the history of mathematics. Euler’s solution didn’t just end a local curiosity—it opened doors to new ways of thinking about connections, paths, and systems.

So next time you look at a city map or a subway system, remember: you’re looking at a real-life graph, and Euler helped us understand how to navigate it.